Skip to main content

Section 2.1 Nonlinear Models

Subsection 1. Evaluate quadratic expressions

When squaring a negative number, don't forget to enclose it in parentheses. For example, if \(x=-4\text{,}\) then

\begin{equation*} x^2=(-4)^2 = (-4)(-4) = 16 \end{equation*}

If we write \(-4^2\text{,}\) then only the 4 is squared, so we have

\begin{equation*} -4^2 = - (4)(4) = -16 \end{equation*}

Subsubsection Examples

Example 2.1.

Evaluate for \(x=-6\text{.}\)

  1. \(\displaystyle 2x^2\)
  2. \(\displaystyle 2-x^2\)
  3. \(\displaystyle (2x)^2\)
  4. \(\displaystyle (2-x)^2\)
Solution

Enclose \(-6\) in parentheses, and follow the order of operations.

  1. Square first, then multiply by 2: \(~~2x^2=2(-6)^2=2(36)=72\)
  2. Square first, then subtract from 2: \(~~2-x^2=2-(-6)^2=2-36=-34\)
  3. Multiply by 2 first, then square: \(~~(2x)^2=[2(-6)]^2=[-12]^2=144\)
  4. Subtract from 2 first, then square: \(~~(2-x)^2=[2-(-6)^2=[8]^2=64\)
Example 2.2.

Make a table of values for \(y=x^2+2x-8\text{,}\) and graph the equation.

Solution

We plot the points from the table and connect them with a smooth curve.

\(x\) \(y\) \(\hphantom{0000}\)
\(-5\) \(7\) \((-5)^2+2(-5)-8=25-10-8\)
\(-4\) \(0\) \((-4)^2+2(-4)-8=16-8-8\)
\(-3\) \(-5\) \((-3)^2+2(-3)-8=9-6-8\)
\(-2\) \(-8\) \((-2)^2+2(-2)-8=4-4-8\)
\(-1\) \(-9\) \((-1)^2+2(-1)-8=1-2-8\)
\(0\) \(-8\) \((0)^2+2(0)-8=0+0-8\)
\(1\) \(-5\) \((1)^2+2(1)-8=1+2-8\)
\(2\) \(0\) \((2)^2+2(2)-8=4+4-8\)
\(3\) \(7\) \((3)^2+2(3)-8=9+6-8\)

parabola y=xsqd+2x-8

Subsubsection Exercises

Evaluate for \(w=-9\)

  1. \(\displaystyle (2w)^2\)
  2. \(\displaystyle 36-(2w)^2\)
  3. \(\displaystyle -2(4-w)^2\)
  4. \(\displaystyle 2-w^2\)
Answer
  1. \(\displaystyle 324\)
  2. \(\displaystyle -288\)
  3. \(\displaystyle -338\)
  4. \(\displaystyle -79\)

Evaluate for \(a=-3,~b=-4\)

  1. \(\displaystyle ab^2\)
  2. \(\displaystyle a-b^2\)
  3. \(\displaystyle (a-b^2)^2\)
  4. \(\displaystyle ab(a^2-b^2)\)
Answer
  1. \(\displaystyle -48\)
  2. \(\displaystyle -19\)
  3. \(\displaystyle 361\)
  4. \(\displaystyle -84\)

Evaluate for \(h=-2,~g=-5\)

  1. \(\displaystyle h^2-2hg+g^2\)
  2. \(\displaystyle (h-g)^2\)
  3. \(\displaystyle h^2-g^2\)
  4. \(\displaystyle (h-g)(h+g)\)
Answer
  1. \(\displaystyle 9\)
  2. \(\displaystyle 9\)
  3. \(\displaystyle -21\)
  4. \(\displaystyle -21\)

Make a table of values for \(y=x^2-x-6\text{,}\) and graph the equation.

\(x\) \(y\)
\(-3\) \(\hphantom{0000}\)
\(-2\) \(\hphantom{0000}\)
\(-1\) \(\hphantom{0000}\)
\(0\) \(\hphantom{0000}\)
\(1\) \(\hphantom{0000}\)
\(2\) \(\hphantom{0000}\)
\(3\) \(\hphantom{0000}\)
\(4\) \(\hphantom{0000}\)
\(5\) \(\hphantom{0000}\)

grid
Answer

\(x\) \(y\)
\(-3\) \(6\)
\(-2\) \(0\)
\(-1\) \(-4\)
\(0\) \(-6\)
\(1\) \(-6\)
\(2\) \(-4\)
\(3\) \(0\)
\(4\) \(6\)
\(5\) \(14\)

parabola

Subsection 2. Use the Pythagorean theorem

If \(a\) and \(b\) are the lengths of the legs of a right triangle and \(c\) is the length of the hypotenuse, then

\begin{equation*} a^2 + b^2 = c^2 \end{equation*}

Note that the theorem is true only for right triangles -- ones that have a 90\(\degree\) angle.

Subsubsection Examples

Example 2.7.

Find the unknown side in the right triangle.

right triangle
Solution

The unknown side is the hypotenuse, so we apply the Pythagorean theorem with \(c=z,~a=12\text{,}\) and \(b=35\text{.}\)

\begin{align*} a^2 + b^2 \amp = c^2\\ 12^2+35^2 \amp =z^2 \amp \amp \blert{\text{Simplify the left side.}}\\ 1369 \amp = z^2 \amp \amp \blert{\text{Take the square root of both sides.}}\\ \pm 37 \amp = z \end{align*}

The length of the hypotenuse is a positive number, so \(z=37\text{.}\)

Example 2.8.

A 25-foot ladder is placed against a wall so that its foot is 7 feet from the base of the wall. How far up the wall does the ladder reach?

Solution

We make a sketch and label the known dimensions, calling the unknown height \(h\text{.}\) The ladder forms the hypotenuse of a right triangle, so we apply the Pythagorean theorem, substituting 25 for \(c\text{,}\) 7 for \(b\text{,}\) and \(h\) for \(a\text{.}\)

\begin{align*} a^2 + b^2 \amp = c^2\\ h^2 + 7^2 \amp = 25^2 \end{align*}
ladder

We solve the equation by extraction of roots:

\begin{align*} h^2 + 49 \amp = 625 \amp \amp \blert{\text{Subtract 49 from both sides.}}\\ h^2 \amp =576 \amp \amp \blert{\text{Extract roots.}}\\ h \amp =\pm \sqrt{576} \amp \amp \blert{\text{Simplify the radical.}}\\ h \amp \pm 24 \end{align*}

The height must be a positive number, so the ladder reaches 24 feet up the wall.

Subsubsection Exercises

A baseball diamond is a square whose sides are 90 feet long. Find the straight-line distance from home plate to second base.

  1. Make a sketch of the situation and label a right triangle.
  2. Write an equation and solve.
Answer
  1. baseball diamond
  2. 127.28 ft

How long a wire is needed to stretch from the top of a 40-foot telephone pole to a point on the ground 20 feet from the base of the pole?

  1. Make a sketch of the situation and label a right triangle.
  2. Write an equation and solve.
Answer
  1. telephone pole and wire
  2. 44.72 ft

Subsection 3. Calculate volume

The volume of a box is measured in cubic units and can be calculated using the formula \(V=lwh\text{,}\) where \(l,~w,\) and \(h\) stand for the length, width, and height of the box. Volume measures the amount of space inside an object by telling us how many blocks 1 unit on a side will fit inside the space. For example, the volume of the box below, whose dimensions are given in centimeters, is

box
\begin{align*} V \amp = lwh \\ \amp = (6)(4)(3) = 72~ \text{cubic centimeters} \end{align*}

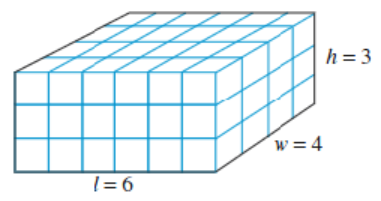
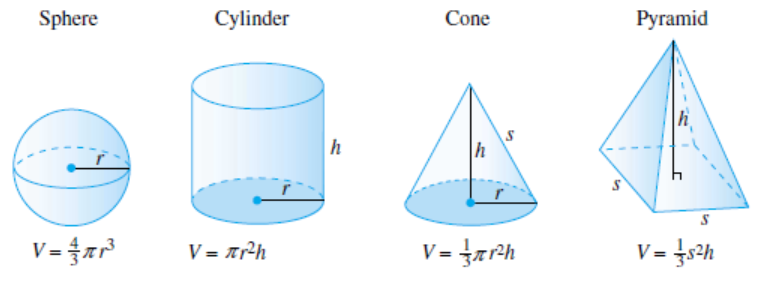
It may seem difficult to measure the inside of a round object like a sphere or a cone in cubic units, but you can imagine filling the object with liquid and then pouring the liquid into a box to measure its volume.

solids

Subsubsection Examples

Example 2.11.

An aquarium is 24 inches long and 10 inches wide. What is the area of its base? How much water is needed to fill it to a depth of 5 inches?

Solution

The area of the base is

\begin{equation*} A=lw=(24~ \text{in})(10~ \text{in})=240~ \text{in}^2 \end{equation*}

To calculate the volume of water, we can multiply the area of the base, \(lw\text{,}\) by the height of the water, \(h\text{.}\)

\begin{equation*} V=(lw)h=Ah=(240~ \text{in}^2)(5~ \text{in})=1200~ \text{in}^3 \end{equation*}
Example 2.12.

The diameter of a spherical wax candle is 5 inches. What is the volume of wax in the candle?

Solution

The radius of the candle is half its diameter, or 2.5 inches. The volume of the candle is

\begin{equation*} V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi(2.5~ \text{in})^3=65.45~\text{in}^3 \end{equation*}

Subsubsection Exercises

Find the volume of a cylindrical water tank whose diameter is 20 feet and whose height is 20 feet.

Answer

6283.2 cubic feet

The diameter of the Earth is about 7920 miles. Find its volume.

Answer

About 260,120,000,000 cubic miles