Skip to main content

Section 2.6 Domain and Range

Subsection 1. Solve equations involving function notation

We must exclude from the domain of a function any values of the input that would cause us to divide by zero or to take the square root of a negative number. To find these values, we usually solve an equation.

We may also solve an equation to find the domain value for a given range value.

Subsubsection Examples

Example 2.59.

Solve \(~3\sqrt{x-4}=15\text{.}\)

Solution

Isolate \(x\) by "undoing" each operation in order: perform the opposite operations.

\begin{align*} 3\sqrt{x-4} \amp = 15 \amp\amp \blert{\text{Divide both sides by 3.}}\\ \sqrt{x-4} \amp = 5 \amp\amp \blert{\text{Square both sides.}}\\ x-4 \amp = 25 \amp\amp \blert{\text{Add 4 to both sides.}}\\ x \amp = 29 \end{align*}

When we square both sides of an equation, we should check for extraneous solutions.

\begin{equation*} 3\sqrt{\alert{29}-4} = 3\sqrt{25} = 3(5)=15 \end{equation*}

Because setting \(x=29\) does not cause us to take the square root of a negative number, the solution is 29.

Example 2.60.

Let \(~f(x)=\dfrac{24}{x-1}\text{.}\) Find \(a\) so that \(f(a) = 4\text{.}\)

Solution

Clear the fraction by multiplying both sides by \((x-1)\text{.}\)

\begin{align*} \dfrac{24}{x-1} \blert{(x-1)} \amp = 4 \blert{(x-1)} \amp\amp \blert{\text{Multiply by}~(x-1).}\\ 24 \amp = 4(x-1) \amp\amp \blert{\text{Divide both sides by 4.}}\\ 6 \amp = x-1 \amp\amp \blert{\text{Add 1 to both sides.}}\\ 7 \amp = x \end{align*}

Substituting 7 into \(x-1\text{,}\) we see that 7 does not cause the denominator to be 0, so 7 is the solution.

Subsubsection Exercises

Solve \(~\sqrt[3]{2x-7}=-2\text{.}\)

Answer
\(x=\dfrac{-1}{2}\)

Solve \(~|x-4|=3\text{.}\)

Answer
\(x=7\) or \(x=1\)

Let \(~~F(x)=5x^3-2~\text{.}\) Find \(t\) so that \(F(t)=8\text{.}\)

Answer
\(x=\sqrt[3]{2}\)

Let \(~~g(x)\dfrac{3}{x^2}~\text{.}\) Find \(b\) so that \(g(b)=16\text{.}\)

Answer
\(b=\pm \dfrac{\sqrt{3}}{4}\)

Subsection 2. Find points on a circle

Recall that the equation for a circle of radius \(r\) centered at the origin is

\begin{equation*} x^2+y^2=r^2 \end{equation*}
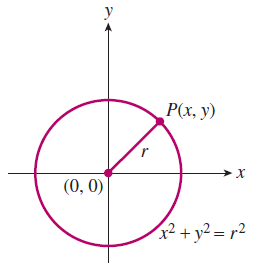
circle

Subsubsection Example

Example 2.65.
  1. Solve the equation \(~x^2+y^2=9~\) for \(y\) to get two functions.
  2. Find two points on the circle that have \(x\)-coordinate \(1\text{.}\)
Solution
  1. \begin{align*} x^2+y^2 \amp = 9 \amp\amp \blert{\text{Subtract}~x^2~\text{from both sides.}}\\ y^2 \amp = 9 - x^2 \amp\amp \blert{\text{Take square roots.}}\\ y \amp = \pm \sqrt{9-x^2} \end{align*}

    The two functions are \(~y = \sqrt{9-x^2}~\) and \(~y = -\sqrt{9-x^2}~\text{.}\)

  2. Substitute \(x=1\) into each equation.

    \begin{equation*} y = \sqrt{9-(\alert{1})^2} = \sqrt{9-1} = \sqrt{8} = 2\sqrt{2} \end{equation*}

    One point is \((1,2\sqrt{2}).\) Similarly, the other point is \((1,-2\sqrt{2}).\)

Subsubsection Exercise

  1. Solve the equation \(~x^2+y^2=100~\) for \(y\) to get two functions.
  2. Find two points on the circle that have \(x\)-coordinate \(-6\text{.}\)
  3. Find two points on the circle that have \(y\)-coordinate \(5\text{.}\)
Answer

  1. \(y = \sqrt{100-x^2}\) and \(y = -\sqrt{100-x^2}\)

  2. \((-6,8)\) and \((-6,-8)\)

  3. \((5\sqrt{3},5)\) and \((-5\sqrt{3},5)\)